[译]SVM核函数RBF的参数
本文翻译自《RBF SVM parameters》。
本例将阐明径向基函数(RBF)做SVM的核函数时参数gamma和C的影响。
直观地,参数gamma定义了单个训练样本的影响大小,值越小影响越大,值越大影响越小。参数gamma可以看作被模型选中作为支持向量的样本的影响半径的倒数。
参数C在误分类样本和分界面简单性之间进行权衡。低的C值使分界面平滑,而高的C值通过增加模型自由度以选择更多支持向量来确保所有样本都被正确分类。
图1是只有两个输入特征和两个可能目标分类(二分类)的简单分类问题在取不同参数值时的决策函数的可视化。注意当有更多特征和目标分类时这种图便画不出来了。
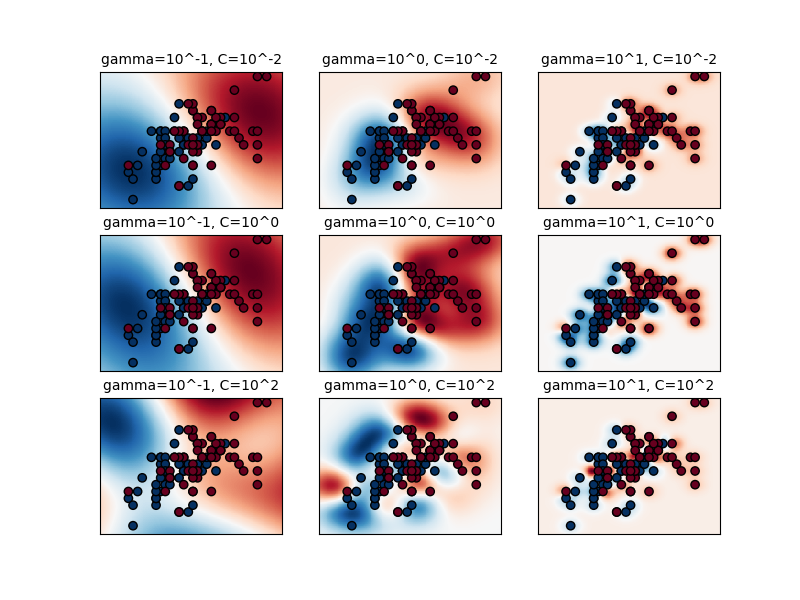
图2是分类器交叉验证的正确率作为C和gamma的函数绘制出的热力图。在这个例子中出于演示目的,我们探索了一个相对较大的参数范围。在实践中,10-3到103的对数范围一般来说是足够的。如果最佳参数位于范围的边界,则可以向该方向扩展范围做进一步的搜索。
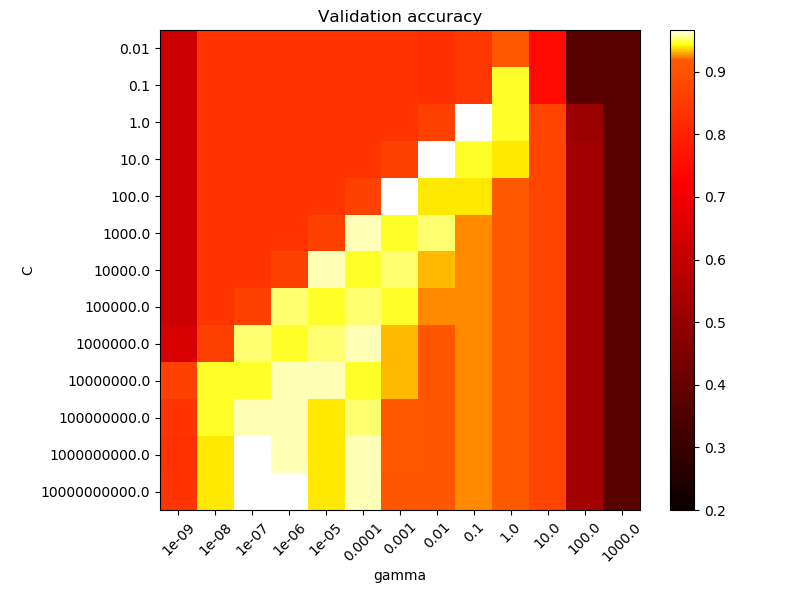
注意到热力图中有一个特殊的彩条,它的中间点的值接近于模型表现最好的得分,这是一眼就可以看到的。
模型的行为对于参数gamma十分敏感。如果参数gamma过大,支持向量的影响半径将小到只能影响到它自己,这时再怎么调整参数C也不能避免过拟合。
当参数gamma非常小时,模型会过于拘束不能捕捉到数据的复杂性或“形状”。任何选中的支持向量的影响区域将包含整个训练集。模型的结果将表现地像是用一组超平面分割两类或多类的高密度中心的线性模型。
至于中间值,我们在图2中可以看到,参数gamma和C的对角线上可以找到好的模型。平滑的模型(更小的gamma值)可以通过选择大量的支持向量(更大的C值)来获得更高的复杂度,于是好的模型便出现在了对角线上。
最后我们也观察到对一些gamma的中间值,当C取非常大的值时依旧可以得到表现良好的模型:没有必要通过限制支持向量的数量来实现正则化。RBF核的半径本身就是一个很好的结构调整器。在实践中仍可能会对通过一个较小的C值来限定支持向量的数目感兴趣,这样就可以使模型使用更少的内存,更快地做出预测。
我们还应该指出随机分割的交叉验证会导致结果得分有细微的不同。通过以计算时间为代价增加CV迭代次数n_splits,可以平滑这种细微的不同。在热力图中增加参数C和gamma的取值步长会降低热力图的分辨率。